Chap 5
- 信源编码
以提高通信有效性为目的的编码。
通常通过压缩信源的冗余度来实现。
采用的一般方法是压缩每个信源符号的平均比特数或信源的码率。
- 信道编码
是以提高信息传输的可靠性为目的的编码。
通常通过增加信源的冗余度来实现。
采用的一般方法是增大码率/带宽
- 密码
是以提高通信系统的安全性为目的的编码。
通常通过加密和解密来实现。
- R’ 编码信息率
编码信息率大于信源的熵,才能实现无失真编码。
定义: R’=l*log(r)/N > H(S) + $\epsilon$
- 编码效率
定义: $\eta$ = $\frac{H(S)}{R’} = \frac{H(S)}{\frac{l}{N}log(r)}$
方差$D[I(s_{i})]$和ε均为定值时,Pe<=δ:
$N \geq \frac{D[I(s_{i})]}{\epsilon^{2} \delta}$
代入最佳情况$\eta = \frac{H(S)}{H(S)+\epsilon}$, thus $\epsilon = \frac{1-\eta}{\eta}H(S)$
$N \geq \frac{D[I(s_{i})]}{ \delta} \frac{\eta^2}{(1-\eta)^2 H(S)^2}$
再对定长码有R’=l*log(r)/N, 对等长r元编码 =>长度 l
- 奇异码
若一组码中有相同的码字,称为奇异码。
- 唯一可译码
若码的任意一串有限长的码符号序列只能被唯一的译成所对应的信源符号序列
- 即时码
任何一个码字后加上若干码元后都不是码组中另一个码字
范围:即时码 < 唯一可译码 < 非奇异码
即时码性质:译码是无须参考后面的码字就可以作出判断
- 即时码的树图构造法
在每个节点上都有r个分枝的树称为整树 =>等长码
否则称为非整树。 =>变长码
定理5.4
对于码符号为 $X = {x_{1},…,x_{q}}$ 的任意即时码,所对应的码长为 $l = {l_{1},…,l_{q}}$ ,必定满足:
$\sum_{i=1}^{q} r^{-l_{i}} \leq 1$
反之,若码长满足上式,则一定存在这样的即时码 。
可以根据即时码的树图构造法来证明。
(对于唯一可译码: (必要条件)必须满足上面的不等式) => 若码长满足上式,则一定存在这样的唯一可译码
若存在一个码长为$l = {l_{1},…,l_{q}}$唯一可译码,则一定存在一个同样长度的即时码
唯一可译变长码的判断法
将码C中所有可能的尾随后缀组成一个集合F,当且仅当集合F中没有包含任一码字,则可判断此码C为唯一可译变长码
steps:
首先观察其是否是非奇异码。若是奇异码则一定不是唯一可译码。
其次观察其是否满足克拉夫特不等式,若不满足一定不是唯一可译码。
将码画成一棵码树图,观察其是否满足即时码的树图的构造,若满足则是唯一可译码。
用萨得纳斯和彼特森设计的判断方法,计算出码中所有可能的尾随后缀集合F,观察F中有没有包含任一码字。
- 若无则为唯一可译码;
- 若有则一定不是唯一可译码
定理5.8 无失真变长信源编码定理(香农第一定理)
离散无记忆信源S的N次扩展信源$S_N$ ,其熵为$H(S_N)$ ,并且编码器的码元符号集为$X={x_1,x_2,…,x_r}$
对信源$S_N$进行编码,总可以找到一种编码方法,构成唯一可译码,
使信源S中每个符号所需要的平均码长满足:
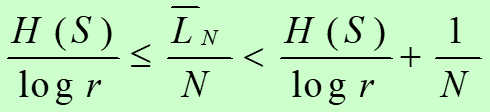
香农第一定理的物理意义
无失真信源编码的实质就是对离散信源进行适当的变换,使变换后新的码符号信源(信道的输入信源)尽可能为等概率分布,以使新信源的每个码符号平均所含的信息量达到最大,
从而使信道的信息传输率R达到信道容量C,实现信源与信道理想的统计匹配
(无失真信源编码定理)
若信道的信息传输率R<=信道容量C,总能对信源的输出进行适当的编码,使的在无噪无损信道上能无差错的以最大信息传输率C
传输信息,若R大于C,则无差错传输是不可能的。