Design Via State Space
formula often used
where T_s represent settling time; T_p represent peak time\
so for the polynomial:

Controllability
The basic equation set: (D alaways = 0)
Introduce the Controller K always 1xN, \
where U always 1x1
So, we obtain
if we could manipulate th poles of $|sI- (A-BK)|$
Thus means
Transformation
Here
We have
That means we have
Compare with
So we have:
Then we have
where X is observer canonical form\
Z is other form (like phase variable form, cascade form)
Observability
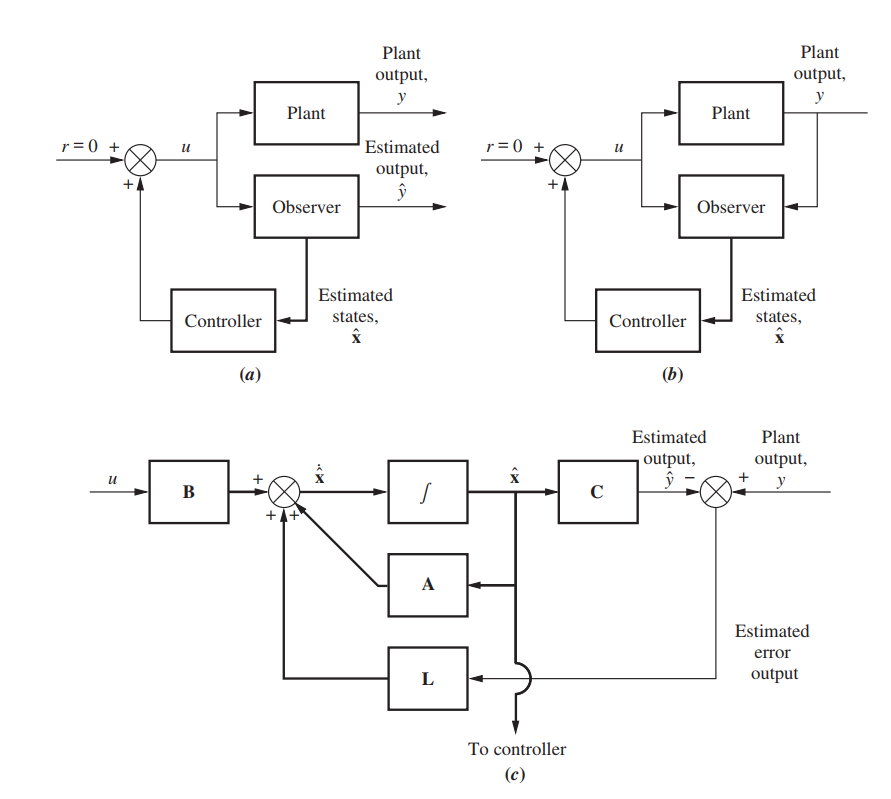
so with
then obtain
define $e_X \equiv (X - \hat{X})$, we have
If all poles of (A-LC) in the left plane
Then we could use $\hat{X}$ to estimate $X$\
regardless the influence of initial value $\hat{X}(0)$ and $X(0)$
Transformation
where X is observer canonical form\
Z is other form (like phase variable form, cascade form)
Then we have
So we have:
Now calculate $O_{Mx}$
So, in conclusion:
Integral Control with 0 Steady-State Error
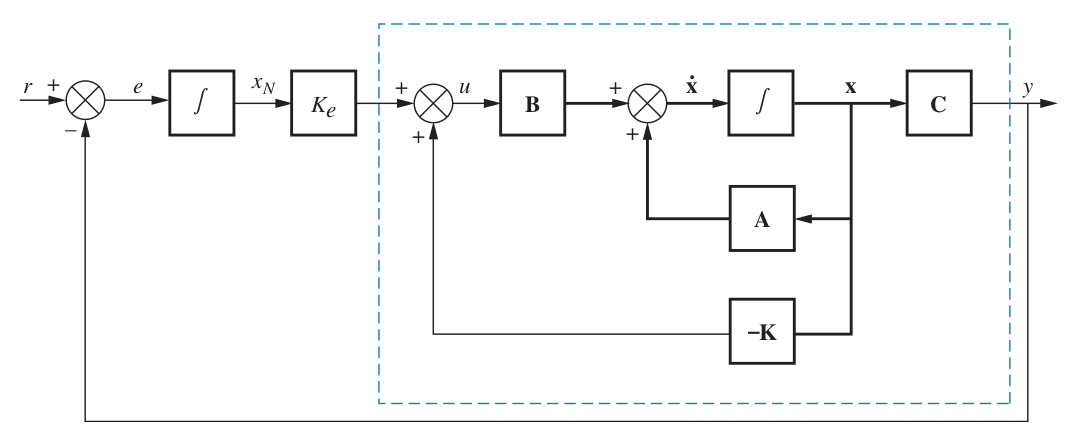
So
Then
Because
so
because
we have
Why zero of T(s) Not change with Controller
we know
why the numurator of G(S), T(s) is the same, because $\forall C$, so must prove
that is mean $\forall A$ (replace sI-A with A)
lemma: Cramer’s Rule
for $AX = B$, where
We have
Here
proof
Another rule $|A+BK| = |A| + Kadj(A)B$
Conclusion
if we introduce K_e
So no matter introduce K and K_e, zeros of T(s) Not change